Custom module example

This tutorial explains how to support new layers in BackPACK.

We will write a custom module and show how to implement first-order extensions, specifically BatchGrad, and second-order extensions, specifically DiagGGNExact.

Let’s get the imports out of our way.

from typing import Tuple

import torch
from einops import einsum
from torch.nn.utils.convert_parameters import parameters_to_vector

from backpack import backpack, extend
from backpack.extensions import BatchGrad
from backpack.extensions.firstorder.base import FirstOrderModuleExtension
from backpack.extensions.module_extension import ModuleExtension
from backpack.extensions.secondorder.diag_ggn import DiagGGNExact
from backpack.hessianfree.ggnvp import ggn_vector_product
from backpack.utils.convert_parameters import vector_to_parameter_list

# make deterministic
torch.manual_seed(0)

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

Custom PyTorch module

In this example, we consider extending our own, very simplistic, layer. It scales the input by a scalar weight in a forward pass. Here is the layer class (see https://pytorch.org/docs/stable/notes/extending.html).

class ScaleModule(torch.nn.Module):
    """Defines the module."""

    def __init__(self, weight: float = 2.0):
        """Store scalar weight.

        Args:
            weight: Initial value for weight. Defaults to 2.0.
        """
        super(ScaleModule, self).__init__()

        self.weight = torch.nn.Parameter(torch.tensor([weight]))

    def forward(self, input: torch.Tensor) -> torch.Tensor:
        """Defines forward pass.

        Args:
            input: The layer input.

        Returns:
            Product of input and weight.
        """
        return input * self.weight

We choose this custom simple layer as its related operations for backpropagation are easy to understand. Of course, you don’t have to define a new layer if it already exists within torch.nn.

It is important to understand though that BackPACK relies on module hooks and therefore can only be extended on the modular level: If your desired functionality is not a torch.nn.Module yet, you need to wrap it in a torch.nn.Module.

First-order extensions

First we focus on BackPACK’s first-order extensions. They don’t backpropagate additional information and thus require less functionality.

Let’s make BackPACK support computing individual gradients for ScaleModule. This is done by the BatchGrad extension. To support the new module, we need to create a module extension that implements how individual gradients are extracted with respect to ScaleModule’s parameter called weight.

The module extension must implement methods named after the parameters passed to the constructor (in this case weight). For a module with additional parametes, e.g. a bias, an additional method named like the parameter has to be added.

Here it goes.

class ScaleModuleBatchGrad(FirstOrderModuleExtension):
    """Extract individual gradients for ``ScaleModule``."""

    def __init__(self):
        """Store parameters for which individual gradients should be computed."""
        super().__init__(params=["weight"])

    def weight(
        self,
        ext: BatchGrad,
        module: ScaleModule,
        g_inp: Tuple[torch.Tensor],
        g_out: Tuple[torch.Tensor],
        bpQuantities: None,
    ) -> torch.Tensor:
        """Extract individual gradients for ScaleModule's ``weight`` parameter.

        Args:
            ext: BackPACK extension that is used.
            module: The module that performed forward pass.
            g_inp: Input gradient tensors.
            g_out: Output gradient tensors.
            bpQuantities: The quantity backpropagated for the extension by BackPACK.
                ``None`` for ``BatchGrad``.

        Returns:
            The per-example gradients w.r.t. to the ``weight`` parameters.
            Has shape ``[batch_size, *weight.shape]``.
        """
        # The ``BatchGrad`` extension supports considering only a sub-set of
        # data in the mini-batch. We will not account for this here for simplicity
        # and therefore raise an exception if this feature is active.
        assert ext.get_subsampling() is None

        show_useful = True
        if show_useful:
            print("Useful quantities:")
            # output is saved under field output
            print("\tmodule.output.shape:", module.output.shape)
            # input i is saved under field input[i]
            print("\tmodule.input0.shape:", module.input0.shape)
            # gradient w.r.t output
            print("\tg_out[0].shape:     ", g_out[0].shape)

        # actual computation
        return einsum(g_out[0], module.input0, "batch d,batch d->batch").unsqueeze(-1)

Note that we have access to the layer’s inputs and outputs from the forward pass, as they are stored by BackPACK. The computation itself basically computes vector-Jacobian-products of the incoming gradient with the layer’s output-parameter Jacobian for each sample in the batch.

Lastly, we need to register the mapping between layer (ScaleModule) and layer extension (ScaleModuleBatchGrad) in an instance of BatchGrad.

# register module-computation mapping
extension = BatchGrad()
extension.set_module_extension(ScaleModule, ScaleModuleBatchGrad())

That’s it. We can now pass extension to a with backpack(...) context and compute individual gradients with respect to ScaleModule’s weight parameter.

Verifying first-order extensions

Here, we verify the custom module extension on a small net with random inputs. Let’s create these.

batch_size = 10
batch_axis = 0
input_size = 4

inputs = torch.randn(batch_size, input_size, device=device)
targets = torch.randint(0, 2, (batch_size,), device=device)

reduction = ["mean", "sum"][1]
my_module = ScaleModule().to(device)
lossfunc = torch.nn.CrossEntropyLoss(reduction=reduction).to(device)

Note

Results of "mean" and "sum" reduction differ by a scaling factor, because the information backpropagated by PyTorch is scaled. This is documented at https://docs.backpack.pt/en/master/extensions.html#backpack.extensions.BatchGrad.

Individual gradients with PyTorch

The following computes individual gradients by looping over individual samples and stacking their gradients.

grad_batch_autograd = []

for input_n, target_n in zip(
    inputs.split(1, dim=batch_axis), targets.split(1, dim=batch_axis)
):
    loss_n = lossfunc(my_module(input_n), target_n)
    grad_n = torch.autograd.grad(loss_n, [my_module.weight])[0]
    grad_batch_autograd.append(grad_n)

grad_batch_autograd = torch.stack(grad_batch_autograd)

print("weight.shape:             ", my_module.weight.shape)
print("grad_batch_autograd.shape:", grad_batch_autograd.shape)

weight.shape:              torch.Size([1])
grad_batch_autograd.shape: torch.Size([10, 1])

Individual gradients with BackPACK

BackPACK can compute individual gradients in a single backward pass. First, extend model and loss function, then perform the backpropagation inside a with backpack(...) context.

my_module = extend(my_module)
lossfunc = extend(lossfunc)

loss = lossfunc(my_module(inputs), targets)

with backpack(extension):
    loss.backward()

grad_batch_backpack = my_module.weight.grad_batch

print("weight.shape:             ", my_module.weight.shape)
print("grad_batch_backpack.shape:", grad_batch_backpack.shape)

Useful quantities:
        module.output.shape: torch.Size([10, 4])
        module.input0.shape: torch.Size([10, 4])
        g_out[0].shape:      torch.Size([10, 4])
weight.shape:              torch.Size([1])
grad_batch_backpack.shape: torch.Size([10, 1])

Do the computation results match?

match = torch.allclose(grad_batch_autograd, grad_batch_backpack)

print(f"autograd and BackPACK individual gradients match? {match}")

if not match:
    raise AssertionError(
        "Individual gradients don't match:"
        + f"\n{grad_batch_autograd}\nvs.\n{grad_batch_backpack}"
    )

autograd and BackPACK individual gradients match? True

Second-order extension

Next, we focus on BackPACK’s second-order extensions. They backpropagate additional information and thus require more functionality to be implemented and a more in-depth understanding of BackPACK’s internals and the quantity of interest.

Let’s make BackPACK support computing the exact diagonal of the generalized Gauss-Newton (GGN) matrix (DiagGGNExact) for ScaleModule.

To do that, we need to write a module extension that implements how the exact GGN diagonal is computed for ScaleModule’s parameter called weight. Also, we need to implement how information is propagated from the layer’s output to the layer’s input.

We need to understand the following details about DiagGGNExact:

1. The extension backpropagates a matrix square root factorization of the loss function’s Hessian w.r.t. its input via vector-Jacobian products.

2. To compute the GGN diagonal for a parameter, we need to multiply the incoming matrix square root of the GGN with the output-parameter Jacobian of the layer, then square it to obtain the GGN, and take its diagonal.

These details vary between different second-order extensions and a good place to get started understanding their details is the BackPACK paper.

We now describe the details for the GGN diagonal.

Definition of the GGN

The GGN is calculated by multiplying the neural network’s Jacobian (w.r.t. the parameters) with the Hessian of the loss function w.r.t. its prediction,

\[\mathbf{G}(\mathbf{\theta}) = (\mathbf{J}_\mathbf{\theta} f_\mathbf{\theta}(x))^\top\; \nabla^2_{f_\mathbf{\theta}(x)} \ell (f_\mathbf{\theta}(x, y) \; (\mathbf{J}_\mathbf{\theta} f_\mathbf{\theta}(x))\,.\]

The Jacobian (left & right of RHS) is the matrix of all first-order derivatives of the function (neural network) w.r.t. the parameters. The Hessian (center of RHS) is the matrix of all second-order derivatives of the loss function w.r.t. the neural network’s output. The GGN (LHS) is a matrix with dimension \(p \times p\) where \(p\) is the number of parameters. Note that in the presence of multiple data (a batch), the GGN is a sum/mean over per-sample GGNs. We will focus on the GGN for one sample, but also handle the parallel computation over all samples in the batch in the code.

Our goal is to compute the diagonal of that matrix. To do that, we will re-write it in terms of a self-outer product as follows: Note that the loss function is convex. Let the neural network’s prediction be \(f_\mathbf{\theta}(x) \in \mathbb{R}^C\) where \(C\) is the number of classes. Due to the convexity of \(\ell\), we can find a symmetric factorization of its Hessian,

\[\exists \mathbf{S} \in \mathbb{R}^{C \times C} \text{ s.t. } \mathbf{S} \mathbf{S}^\top = \nabla^2_{f_\mathbf{\theta}(x)} \ell (f_\mathbf{\theta}(x), y)\,.\]

For our purposes, we will use a loss that is already supported within BackPACK, and there we don’t need to be concerned how to compute this factorization.

With that, we can define \(\mathbf{V}= (\mathbf{J}_\mathbf{\theta} f_\mathbf{\theta}(x))^\top\;\mathbf{S}\) and write the GGN as

\[\mathbf{G}(\mathbf{\theta}) = \mathbf{V} \mathbf{V}^\top\,.\]

Instead of computing the GGN, we will compute \(\mathbf{V}\) by backpropagating \(\mathbf{S}\) via vector-Jacobian products, then square-and-take-the-diagonal to obtain the GGN’s diagonal.

Backpropagation for the GGN diagonal

To break down the multiplication with \((\mathbf{J}_\mathbf{\theta} f_\mathbf{\theta}(x))^\top\) to the per-layer level, we will use the chain rule.

Consider the following computation graph, where \(x = x^{(0)}\):

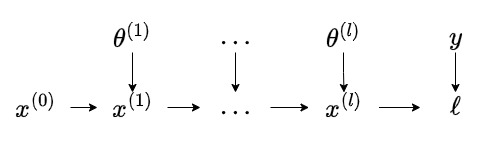
Each node in the graph represents a tensor. The arrows represent the flow of information and the computation associated with the incoming and outgoing tensors: \(f_{\mathbf{\theta}^{(k)}}^{(k)}(x^{(k)}) = x^{(k+1)}\). The intermediates correspond to the outputs of the neural network layers.

The parameter vector \(\mathbf{\theta}\) contains all NN parameters, flattened and concatenated over layers,

\[\begin{split}\mathbf{\theta} = \begin{pmatrix} \mathbf{\theta}^{(1)} \\ \mathbf{\theta}^{(2)} \\ \vdots \\ \mathbf{\theta}^{(l)} \end{pmatrix}\,.\end{split}\]

The Jacobian inherits this structure and is a stack of Jacobians of each layer,

\[\begin{split}(\mathbf{J}_\mathbf{\theta} f_\mathbf{\theta}(x))^\top = \begin{pmatrix} (\mathbf{J}_{\mathbf{\theta}^{(1)}} f_{\mathbf{\theta}}(x))^\top \\ (\mathbf{J}_{\mathbf{\theta}^{(2)}} f_{\mathbf{\theta}}(x))^\top \\ \vdots \\ (\mathbf{J}_{\mathbf{\theta}^{(l)}} f_\mathbf{\theta}(x))^\top \end{pmatrix}\,.\end{split}\]

The same holds for the matrix \(\mathbf{V}\),

\[\begin{split}\mathbf{V} = \begin{pmatrix} \mathbf{V}_{\mathbf{\theta}^{(1)}} \\ \mathbf{V}_{\mathbf{\theta}^{(2)}} \\ \vdots \\ \mathbf{V}_{\mathbf{\theta}^{(l)}} \end{pmatrix} = \begin{pmatrix} (\mathbf{J}_{\mathbf{\theta}^{(1)}} f_{\mathbf{\theta}}(x))^\top \mathbf{S} \\ (\mathbf{J}_{\mathbf{\theta}^{(2)}} f_{\mathbf{\theta}}(x))^\top \mathbf{S} \\ \vdots \\ (\mathbf{J}_{\mathbf{\theta}^{(l)}} f_\mathbf{\theta}(x))^\top \mathbf{S} \end{pmatrix}\,.\end{split}\]

With the chain rule recursions

\[(\mathbf{J}_{\mathbf{\theta}^{(k)}} f_{\mathbf{\theta}}(x))^\top = (\mathbf{J}_{\mathbf{\theta}^{(k)}} x^{(k)})^\top \;(\mathbf{J}_{x^{(k)}} f_{\mathbf{\theta}}(x))^\top\]

and

\[(\mathbf{J}_{x^{(k-1)}} f_{\mathbf{\theta}}(x))^\top = (\mathbf{J}_{x^{(k-1)}} x^{(k)})^\top \;(\mathbf{J}_{x^{(k)}} f_{\mathbf{\theta}}(x))^\top\]

we can identify the following recursions for the blocks of \(\mathbf{V}\):

\[\mathbf{V}_{\mathbf{\theta}^{(k)}} = (\mathbf{J}_{\mathbf{\theta}^{(k)}} x^{(k)})^\top \mathbf{V}_{x^{(k)}}\]

and

\[\mathbf{V}_{x^{(k-1)}} = (\mathbf{J}_{x^{(k-1)}} x^{(k)})^\top \mathbf{V}_{x^{(k)}}\,.\]

The above two recursions are the backpropagations performed by BackPACK’s DiagGGNExact. Layer \(k\) receives the backpropagated quantity \(\mathbf{V}_{x^{(k)}}\), then (i) computes \(\mathbf{V}_{\mathbf{\theta}^{(k)}}\), then \(\mathrm{diag}(\mathbf{V}_{\mathbf{\theta}^{(k)}} \mathbf{V}_{\mathbf{\theta}^{(k)}}^\top)\), which is the GGN diagonal for the layer’s parameters, and (ii) computes \(\mathbf{V}_{x^{(k-1)}}\) which is sent to its parent layer \(k-1\) which proceeds likewise.

Implementation

Now, let’s create a module extension that specifies two methods: Step (i) from above is implemented by a function whose name matches the layer parameter’s name (weight in our case). Step (ii) is implemented by a function named backpropagate.

class ScaleModuleDiagGGNExact(ModuleExtension):
    """Backpropagation through ``ScaleModule`` for computing the GGN diagonal."""

    def __init__(self):
        """Store parameter names for which the GGN diagonal will be computed."""
        super().__init__(params=["weight"])

    def backpropagate(
        self,
        ext: DiagGGNExact,
        module: ScaleModule,
        grad_inp: Tuple[torch.Tensor],
        grad_out: Tuple[torch.Tensor],
        bpQuantities: torch.Tensor,
    ) -> torch.Tensor:
        """Propagate GGN diagonal information from layer output to input.

        Args:
            ext: The GGN diagonal extension.
            module: Layer through which to perform backpropagation.
            grad_inp: Input gradients.
            grad_out:: Output gradients.
            bpQuantities: Backpropagation information. For the GGN diagonal
                this is a tensor V of shape ``[C, *module.output.shape]`` where
                ``C`` is the neural network's output dimension and the layer's
                output shape is typically something like ``[batch_size, D_out]``.

        Returns:
            The GGN diagonal's backpropagated quantity V for the layer input.
            Has shape ``[C, *layer.input0.shape]``.
        """
        # The GGN diagonal extension supports considering only a sub-set of
        # data in the mini-batch. We will not account for this here for simplicity
        # and therefore raise an exception if this feature is active.
        assert ext.get_subsampling() is None

        # Layer:
        # - Input to the layer has shape ``[batch_size, D_in]``
        # - Output of the layer has shape ``[batch_size, D_out]``

        # Loss function:
        # - Neural networks prediction has shape ``[batch_size, C]``

        # Quantity backpropagated by ``DiagGGNExact`` has shape
        # ``[C, batch_size, D_out]`` imagine this as a set of ``C`` vectors
        # which all have the same shape as the layer's output that represent
        # the rows of the incoming V.

        # What we need to to do:
        # - Take each of the C vectors
        # - Multiply each of them with the layer's output-input Jacobian.
        #   The result of each VJP will have shape ``[batch_size, D_in]``
        # - Stack them back together into a tensor of shape
        #   ``[C, batch_size, D_in]`` that represents the outgoing V

        input0 = module.input0
        output = module.output
        weight = module.weight
        V_out = bpQuantities

        C = V_out.shape[0]
        batch_size, D_in = input0.shape
        assert V_out.shape == (C, *output.shape)

        show_useful = True
        if show_useful:
            print("backpropagate: Useful quantities:")
            print(f"              module.output.shape: {output.shape}")
            print(f"              module.input.shape: {input0.shape}")
            print(f"              V_out.shape: {V_out.shape}")
            print(f"              V_in.shape: {(C, *input0.shape)}")

        V_in = torch.zeros(
            (C, batch_size, D_in), device=input0.device, dtype=input0.dtype
        )

        # forward pass computation performs: ``X * weight``
        # (``[batch_size, D_in] * [1] [batch_size, D_out=D_in]``)
        for c in range(C):
            V_in[c] = bpQuantities[c] * weight
        # NOTE We could do this more efficiently with the following:
        # V_in = V_out * weight
        assert V_in.shape == (C, *input0.shape)

        return V_in

    def weight(
        self,
        ext: DiagGGNExact,
        module: ScaleModule,
        g_inp: Tuple[torch.Tensor],
        g_out: Tuple[torch.Tensor],
        bpQuantities: torch.Tensor,
    ) -> torch.Tensor:
        """Extract the GGN diagonal for the ``weight`` parameter.

        Args:
            ext: The BackPACK extension.
            module: Module through which to perform backpropagation.
            grad_inp: Input gradients.
            grad_out: Output gradients.
            bpQuantities: Backpropagation information. For the GGN diagonal
                this is a tensor V of shape ``[C, *module.output.shape]`` where
                ``C`` is the neural network's output dimension and the layer's
                output shape is typically something like ``[batch_size, D_out]``.

        Returns:
            The GGN diagonal w.r.t. the layer's ``weight``.
            Has shape ``[batch_size, *weight.shape]``.
        """
        input0 = module.input0
        output = module.output
        weight = module.weight
        V_out = bpQuantities

        C = bpQuantities.shape[0]
        assert V_out.shape == (C, *output.shape)

        show_useful = True
        if show_useful:
            print("weight: Useful quantities:")
            print(f"       module.output.shape {output.shape}")
            print(f"       module.input.shape {input0.shape}")
            print(f"       module.weight.shape {weight.shape}")
            print(f"       bpQuantities.shape {bpQuantities.shape}")
            print(f"       returned.shape {weight.shape}")

        # forward pass computation performs: ``X * weight``
        # (``[batch_size, D_in] * [1] = [batch_size, D_out]``)
        V_theta = einsum(V_out, input0, "c batch d, batch d -> c batch")
        # compute diag( V_theta @ V_theta^T )
        weight_ggn_diag = einsum(V_theta, V_theta, "c batch, c batch ->").unsqueeze(0)

        assert weight_ggn_diag.shape == weight.shape
        return weight_ggn_diag

After we have implemented the module extension we need to register the mapping between layer (ScaleModule) and layer extension (ScaleModuleDiagGGNExact) in an instance of DiagGGNExact.

extension = DiagGGNExact()
extension.set_module_extension(ScaleModule, ScaleModuleDiagGGNExact())

We can then use this extension to compute the exact GGN diagonal for ``ScaleModule``s.

Verifying second-order extensions

Here, we verify the custom module extension on a small net with random inputs. First, the setup:

batch_size = 10
input_size = 4

inputs = torch.randn(batch_size, input_size, device=device)
targets = torch.randint(0, 2, (batch_size,), device=device)

reduction = ["mean", "sum"][1]

my_module = ScaleModule().to(device)
lossfunc = torch.nn.CrossEntropyLoss(reduction=reduction).to(device)

As ground truth, we compute the GGN diagonal using GGN-vector products which exclusively rely on PyTorch’s autodiff:

params = list(my_module.parameters())
ggn_dim = sum(p.numel() for p in params)
diag_ggn_flat = torch.zeros(ggn_dim, device=inputs.device, dtype=inputs.dtype)

outputs = my_module(inputs)
loss = lossfunc(outputs, targets)

# compute GGN-vector products with all one-hot vectors
for d in range(ggn_dim):
    # create unit vector d
    e_d = torch.zeros(ggn_dim, device=inputs.device, dtype=inputs.dtype)
    e_d[d] = 1.0
    # convert to list format
    e_d = vector_to_parameter_list(e_d, params)

    # multiply GGN onto the unit vector -> get back column d of the GGN
    ggn_e_d = ggn_vector_product(loss, outputs, my_module, e_d)
    # flatten
    ggn_e_d = parameters_to_vector(ggn_e_d)

    # extract the d-th entry (which is on the GGN's diagonal)
    diag_ggn_flat[d] = ggn_e_d[d]

print(f"Tr(GGN): {diag_ggn_flat.sum():.3f}")

Tr(GGN): 1.567

Now we can use BackPACK to compute the GGN diagonal:

my_module = extend(my_module)
lossfunc = extend(lossfunc)

outputs = my_module(inputs)
loss = lossfunc(outputs, targets)

with backpack(extension):
    loss.backward()

diag_ggn_flat_backpack = parameters_to_vector(
    [p.diag_ggn_exact for p in my_module.parameters()]
)
print(f"Tr(GGN, BackPACK): {diag_ggn_flat_backpack.sum():.3f}")

weight: Useful quantities:
       module.output.shape torch.Size([10, 4])
       module.input.shape torch.Size([10, 4])
       module.weight.shape torch.Size([1])
       bpQuantities.shape torch.Size([4, 10, 4])
       returned.shape torch.Size([1])
Tr(GGN, BackPACK): 1.567

Finally, let’s compare the two results.

match = torch.allclose(diag_ggn_flat, diag_ggn_flat_backpack)
print(f"Do manual and BackPACK GGN match? {match}")

if not match:
    raise AssertionError(
        "Exact GGN diagonals do not match:"
        + f"\n{diag_ggn_flat}\nvs.\n{diag_ggn_flat_backpack}"
    )

Do manual and BackPACK GGN match? True

That’s all for now.